steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
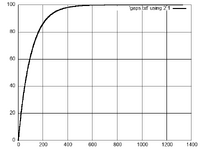
One of the tests to evaluate a random number generator is the gap test. For a uniform distribution of integers 0-100 for a given number the gaps between occurrences of the number are found and the cumulative distribution is plotted.
I would have thought the distribution would have been normal or uniform as a guess, but it is exponential.
I do not know enough to directly work out why, a problem to chew on for somebody with better math.
Given a uniformly random distribution of integers length n derive why the di9stribution of distances between occurrences of a single number is exponentially distributed.

 en.wikipedia.org
Solution would be an exponential distribution p(x) = (1/average)*e^(-x/average)
en.wikipedia.org
Solution would be an exponential distribution p(x) = (1/average)*e^(-x/average)
The code uses the C++ built in mt19937 generator.
Gnuplot cd.plt
set term windows background rgb "white" title "SIGNALS" fontscale 1
reset
set grid lt 1 lw 1 lc rgb "black" dashtype solid
set yrange[*:100]
set xrange[0:*]
plot 'gaps.txt' using 2:1 with lines ls 4 lt -1 lw 3
show grid
I would have thought the distribution would have been normal or uniform as a guess, but it is exponential.
I do not know enough to directly work out why, a problem to chew on for somebody with better math.
Given a uniformly random distribution of integers length n derive why the di9stribution of distances between occurrences of a single number is exponentially distributed.

Exponential distribution - Wikipedia
The code uses the C++ built in mt19937 generator.
Gnuplot cd.plt
set term windows background rgb "white" title "SIGNALS" fontscale 1
reset
set grid lt 1 lw 1 lc rgb "black" dashtype solid
set yrange[*:100]
set xrange[0:*]
plot 'gaps.txt' using 2:1 with lines ls 4 lt -1 lw 3
show grid
Code:
#include <random>
void gap_test(void){
cout<<"gap test"<<endl;
long long i,n = pow(10,7);
double aver,median;
int *y = new int[n];
int *gaps = new int[100000];
double *cd = new double[100000];
int hi = 100,lo = 0;
mt19937 rand_gen(time(NULL));
uniform_int_distribution<unsigned int> dist (lo,hi);
for(i=0;i<n;i++) y[i] = dist(rand_gen);
int gap0,gap1,s = 0,ngaps=0;
int delta,max =0,min = n;
int num =33;
for(i=0;i<n;i++){if(y[i]==num)gap0=i;break;}
gap1 = gap0;
for(i=gap0+1;i<n;i++){
if(y[i] == num){
delta = i-gap1;
s += delta;
if(delta > max)max = delta;
if(delta<min)min = delta;
gap1= i;
gaps[ngaps] = delta;
ngaps++;
}
}
for(i=0;i<ngaps;i++)cd[i] = 100*double(i)/double(ngaps);
sort(&gaps[0],&gaps[ngaps]);
aver = double(s)/double(ngaps);
printf("n gaps %d\n",ngaps);
printf("number %d lo %d hi %d\n",num,lo,hi);
printf("min gap %d max gap %d\n",min,max);
printf("average gap %f median %f\n",aver,log(2)*aver);
FILE *p = fopen("gap_test.txt","w");
fprintf(p,"n gaps %d\n",ngaps);
fprintf(p,"number %d lo %d hi %d\n",num,lo,hi);
fprintf(p,"min gap %d max gap %d aver gap %.5f\n",min,max,aver);
fclose(p);
p = fopen("gaps.txt","w");
for(i=0;i<ngaps;i++)fprintf(p," %2.6f\t %10d\n",cd[i],gaps[i]);
fclose(p);
system("cd.plt");
}
Last edited: